时频表示(Time Frequency Representation)
时频表示基于短时傅里叶变换(Short-Time Fourier Transfrom,STFT)。
同时使用时间、频率域分析的原因：
脑电信号的非稳定特性
缺点
在所有的频率范围有统一的时频分辨率，然而我们感兴趣的脑电的频率通常小于30Hz,很多伪迹的频率小于10Hz，这就需要在低频范围有STFT(短时傅里叶变换)不能提供的高频分辨率。
问题的解决
采用基于小波的方法-小波变换（适合为脑电信号的每一个频带提供相应的分辨率）
机器学习 | 机器学习中分类标签次数统计代码模板
机器学习中分类标签次数统计代码模板
在使用机器学习的算法进行分类时，很多时候我们需要去统计各个分类标签在数据集中出现的次数，它的实现代码模板如下：
def class_count(class_list): # class_list:数据集数据的所有标签列表
# 存放各个分类出现的次数
class_counts = {}
# 统计class_list中每个元素出现的次数
for cla in class_list:
if cla not in class_counts.keys():
class_counts[cla] = 0
class_counts[cla] += 1
# 排序
sorted_class_count = sorted(class_counts.items(), key=operator.itemgetter(1), reverse=True)
return sorted_class_count
机器学习 | 决策树
决策树
决策树(Decision Tree)是一种基本的分类与回归方法。决策树由结点(Node)和有向边(Directed Edge)组成。结点有两种类型：内部结点(Internnal Node)和叶结点(Leaf Node)。内部结点表示一个特征或属性，叶结点表示一个类。决策树还有一个唯一的根结点(Root Node)。
我们可以把决策树看成一个if-then规则的集合,将决策树转换成if-then规则的过程是这样的：
由决策树的根结点到叶结点的每一条路径构建一条规则；路径上内部结点的特征对应着规则的条件，而叶结点对应着规则的结论。
决策树的路径或其对应的if-then规则集合具有一个重要性质：互斥并且完备(每一个实例都只能被一条路径或一条规则所覆盖(覆盖：实例的特征与路径上的特征一致或实例满足规则的条件))。
决策树做预测的步骤
1.收集数据
2.准备数据(将收集的数据按照一定规则整理出来,方便后续进行处理)
3.分析数据(在决策树构造完成后，检查决策树图形是否符合预期)
4.训练算法(构造决策树/决策树学习—>构造一个决策树的数据结构)
5.测试算法(使用经验树计算错误率。当错误率达到可接受范围，这个决策树就可以投放使用)
6.使用算法(决策树可以更好地理解数据的内在含义)
如何构建决策树？—构建决策树的3个步骤
1.特征选择
特征选择就是决定用哪个特征来划分特征空间
特征选择在于选取训练数据具有分类能力的特征
特征选择的标准：信息增益(Information Gain)/信息增益比。信息增益：在划分数据集之后信息发生的变化。
Note:信息增益最高的特征是最好的选择
1.1香农熵(熵)-信息论之父克劳德.香农：集合信息的度量方式。
熵定义为信息的期望值。在信息论与概率论中，熵是表示随机变脸不确定性的度量。如果待分类的事物可能划分在多个分类之中，则符号xi的信息定义为：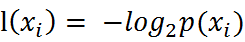
其中p(xi)是该分类的概率。
通过上式，我们可以得到所有类别的信息。为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值(数学期望-反应随机变量平均取值的大小)，公式如下：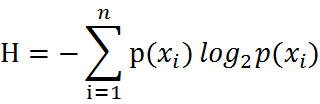
其中n是分类的数目。熵越大，随机变量的不确定性就越大。
当熵中的概率由数据估计(特别是最大似然估计-Maximum Likelihood Estimation)得到时，所对应的熵称为经验熵(Empirical Entropy)
我们定义样本数据表中的数据为训练数据集D，则训练数据集D的经验熵为H(D)，|D|表示其样本容量，及样本个数。设有K个类Ck, = 1,2,3,…,K,|Ck|为属于类Ck的样本个数，因此经验熵公式就可以写为 ：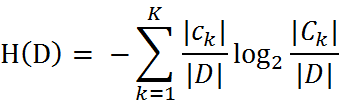
1.2信息增益
如何选择特征，需要看信息增益。也就是说，信息增益是相对特征而言的，信息增益越大，特征对最终的分类结果影响也就越大，我们就应该选择对最终分类结果影响最大的那个特征作为我们的分类特征。
条件熵H(Y|X)表示在一直随机变量X的条件下随机变量Y的不确定性，随机变量X给定条件下随机变量Y的条件熵(Conditional Entropy)H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：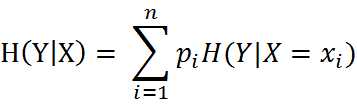
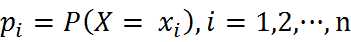
当条件熵中的概率由数据估计(特别是极大似然估计)得到时，岁对应的条件熵称为条件经验熵(empirical conditional entropy)。
特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即：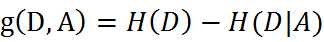
Note:一般地，熵H(D)与条件熵H(D|A)之差称为互信息(mutual information)。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
设特征A有n个不同的取值{a1,a2,···,an}，根据特征A的取值将D划分为n个子集{D1,D2，···,Dn}，|Di|为Di的样本个数。记子集Di中属于Ck的样本的集合为Dik，即Dik = Di ∩ Ck，|Dik|为Dik的样本个数。于是经验条件熵的公式可以些为：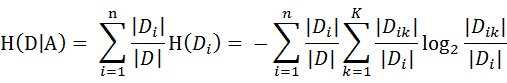
总结
决策树的一些优点
1.易于理解和解释。决策树可以可视化。2.几乎不需要数据预处理。其他方法经常需要数据标准化，创建虚拟变量和删除缺失值。决策树还不支持缺失值。
3.使用树的花费(例如预测数据)是训练数据点(data points)数量的对数。
4.可以同时处理数值变量和分类变量。其他方法大都适用于分析一种变量的集合。
5.可以处理多值输出变量问题
6.使用白盒模型.如果一个情况被观察到，使用逻辑判断容易表示这种规则。相反，如果是黑盒模型(例如人工神经网络)，结果会非常难解释。
7.即使对真实模型来说，假设无效的情况下，也可以较好的使用
决策树的一些缺点
1.决策树学习可能创建一个过于复杂的树，并不能很好的预测数据。也就是过拟合。修剪机制（现在不支持），设置一个叶子节点需要的最小样本数量，或者数的最大深度，可以避免过拟合。2.决策树可能是不稳定的，因为即使非常小的变异，可能会产生一颗完全不同的树。这个问题通过decision trees with an ensemble来缓解。
3.概念难以学习，因为决策树没有很好的解释他们，例如，XOR, parity or multiplexer problems(奇偶校验或多路复用器问题)。
4.如果某些分类占优势，决策树将会创建一棵有偏差的树。因此，建议在训练之前，先抽样使样本均衡。
ICA | 鸡尾酒宴会问题
鸡尾酒宴会问题
鸡尾酒宴会问题是独立成分分析(Indepen Compon Analysis)的经典问题。
问题描述
假设在party中有n个人，他们可以同时说话，我们也在房间中一些角落里共放置了n个声音接收器（Microphone）用来记录声音。宴会过后，我们从n个麦克风中得到了一组数据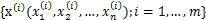
，i表示采样的时间顺序，也就是说共得到了m组采样，每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
将第二个问题细化一下，有n个信号源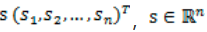
,每一维都是一个人的声音信号，每个人发出的声音信号独立。A是一个未知的混合矩阵（mixing matrix），用来组合叠加信号s，那么
X = AS
X的意义在上文解释过，这里的x不是一个向量，是一个矩阵。其中每个列向量是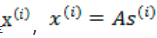
表示成图就是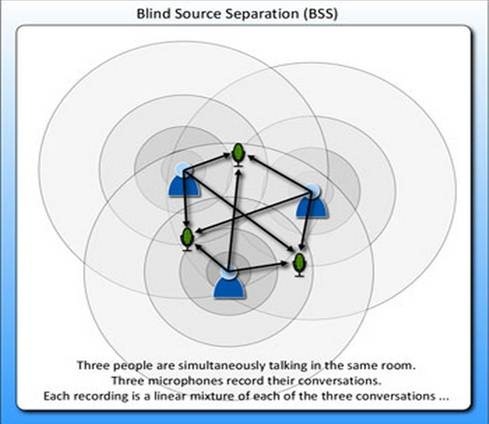
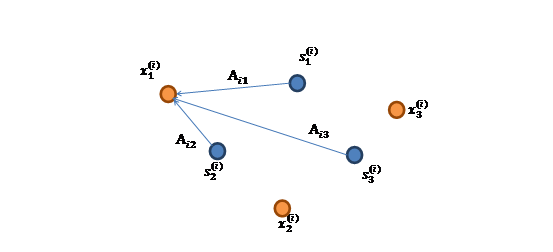
x(i)的每个分量都由s(i)的分量线性表示。A和s都是未知的，x是已知的，我们要想办法根据x来推出s。这个过程也称作为盲信号分离。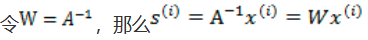
将W表示成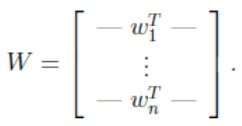
其中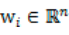
,起始就是将wi携程行向量形式。那么得到：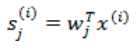
脑电分类 | 机器学习实现脑电分类
伪迹移除 | 盲源分离和独立成分分析
盲源分离(BSS)和独立成分分析(ICA)
BSS
盲源分离是最流行的伪迹检测/移除方法之一，其目的是提取混合信号中独立的未知的源信号；同时尽可能在对源信号和混合通道没有或者有非常有限的了解下尽可能仅通过在每一个通道的输出观测到的混合信号来估计未知的混合通道。盲源分离包括ICA(独立成分分析)、CCA(典型成分分析)、MCA(形态成分分析)三种方法。
数学表示式：
X = AS + N
S’ = WX
其中,X表示观测到的信号(假设X为若干源信号和噪声信号的混合),N代表噪声信号，A为系数矩阵，W也为系数矩阵（需要对W矩阵进行估计），S’为S的估计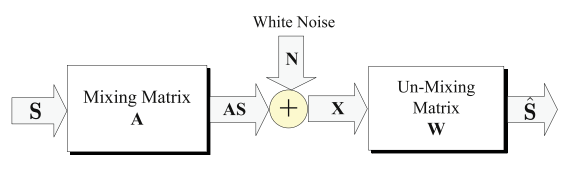
ICA
独立成分分析是盲源分离的一个特例，它假设组成观测信号的若干源信号是线性独立的。
基于ICA的伪迹检测和去除方法存在的问题
1.非自动的
2.需要人为介入去除观察到的伪迹
基于ICA的伪迹检测和去除方法的自动化
1.ICA+WT(Wavelet Transform,小波变换)
2.ICA+EMD(Empirical Mode Decomposition,经验模态分解)
3.使用分类器，例如SVM(Support Vector Machine,支持向量机-一种机器学习算法)
4.参考信号辅助
缺点
1.伪迹独立成分仍然可能包含残余的神经信号导致神经信号的失真
2.不能用于单通道数据
3.不适合实时应用