Logistic回归可视化主要代码

import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1,ycord1,s=20,c='red',marker='s',alpha=0.5)
ax.plot(x,y)
plt.title()
plt.xlabel()
plt.ylabel()
plt.show()

多个坐标轴可视化主要代码

在机器学习算法的使用中，我们需要使用多个坐标轴对一些过程数据/预测结果等进行可视化以便于进一步的分析，它的主要python代码如下：

Logistic回归

Logistic回归是一种分类算法，通常用于二分类问题(例如：明天是否会下雨)，但也可以用于多分类问题。

朴素贝叶斯

朴素贝叶斯算法(Naive Bayes)是有监督(supervised)的学习算法，解决的是分类问题(例如：客户是否流失、是否值得投资、信用等级评定等多分类问题)

python中的iter()与next()

可迭代对象(Iterable)：可以直接作用于for循环的对象

分类：
1.集合数据类型 list、tuple、dict、set、str
2.generator(包括生成器和带yield的generator function)
Note:生成器不但可以作用于 for 循环，还可以被 next() 函数不断调用并返回下一个值

生成器都是Iterator,但list、tuple、dict、str、set虽然是Iterable,却不是Iterator，可以使用iter()函数把list…Iterable编程Iterator

伪迹去除方法比较总结

1.(定性比较 or 定量比较)很难对不同伪迹去除方法基于它们去除伪迹的能力进行一个比较，通常只能做一个定性(qualitative)的比较
2.(自动 or 半自动)很多基于EEG的应用需要自动信息处理，尤其是一些对在线/实时(需要效率很高的算法和足够低的计算复杂度)有要求的应用。基于BSS(盲源分离)的方法通常是半自动的,因为伪迹成分的识别需要一些训练或参数选择/调整。涉及ICA的伪迹检测/去除方法需要另一个方法才能实现全过程的自动
3.(单通道 or 多通道)基于盲源分离的方法需要多通道才能起作用，通道数量越多，越能很好的分离出单个的源(这种方法不能用于低通道 e.g. 4-6或者基于单通道的应用)。基于小波变换和经验模态分解的方法可以通过将单个数据序列分解为多个成分进行单通道分析。
4.(参考信号)大多数方法需要参考信号。

PCA

PCA is a type of spatial filter that transforms the time domain datasets into a different space by rotating axes in an N-dimensional space(where n is the number of variables or EEG channels) such that each dimension in the new space has minimum variance and the axes are orthogonal to each other.

PCA reduces data dimension and highlights specific features of data,which is usually difficult to identify in the spatially unfiltered data as the new components are created by weighted combinations of all EEG channels.

One important limitation of PCA (or SVD)

it fails to separate/identify ocular or similar artifacts from
EEG when amplitudes are comparable since PCA depends on
the higher order statistical property

Adaptive Filter

Adaptive Filter is a system with a linear filter that has a transfer function controlled by variable parameters and a means to adjust those parameters according to an optimization algorithm.The filter weights can adapt based on the feedback from output of the system and it requires a reference input o compare the desired output with the observed output.

The use of adaptive filter for EOG artifact removal

where s[n] is observed signal,x[n] is original EEG,r[n] is artifact,x’[n] is artifact-free EEG.

EMD

EMD is an empirical and data-driven method developed to perform on non-stationary,non-linear, stochastic processes(it is ideally suitable for EEG signal analysis and processing)

Disadvantages:

1.the computational complexity is quite heavy(not suitable for online application)
2.the theory behind EMD is still not complete and so far used in empirical studies(difficult to predict its robustness in all EEG recordings)

EMD Algorithm

EMD algorithm decomposes a signal,s[n] into a sum of the band-limited components/functions,c[n] called intrinsic mode funciton(IMF) with well defined instantaneous frequencies.

Two Basic Conditions to be an IMF

1.the numberof extrema must be equal(or at most may differ by one) to the number of zero crossings
2.any point,the mean value of the two envelopes defined by the local maxima and the local minima has to be zero

The General Process flow of EMD Algorithm

Input: data sequence s[n]
1.Identify all the local extrema
2.Separately connect all the maxima and minima with natural cubic spline lines to form the upper,u[n],and lower,l[n],envelopes.
3.Find the mean of the envolopes as z[n]=[u[n]+l[n]]/2
4.Take the difference between the data and the mean as the proto-IMF,h[n]=s[n]-z[n]
5.Check the proto-IMF against the definition of IMF and the stoppage criterion to determine if it is an IMF
6.If the proto-IMF does not satisfy the definition,repeat step 1 to 5 on h[n] as many times as needed till it satisfies the definition
7.If the proto-IMF does satisfy the definition,assign the proto-IMF as an IMF component,c[n]
8.Repeat the operation step 1 to 7 on the residue,q[n]=s[n]-c[n],as the data
9.The operation ends when the residue contains no more than one extrema

EEMD(enhanced version of EMD)

EEMD it inspired from the fact that EMD is very sensitive to noise,which often leads to mode mixing complication.
EEMD is proposed which uses an average number of ensembles(IMFs) from EMD as the optimal IMFs thus it provides a noise-assisted data analysis method.

小波变换(Wavelet Transform,WT)

小波变化是一个时间尺度的表示方法，它把信号分解成时间和尺度的基函数(母小波基函数的扩展/变体)

一些基于小波理论的技术

1.wavelet packets
2.wavelet approximation and decomposition
3.discrete and continuous wavelet transform
…
其中，最常用的技术是离散小波变换(Discrete Wavelet Transform);
离散小波变换是由离散输入的连续小波变换得到的；
离散小波变换将信号输入到低通滤波器中，得到低频分量，进入高通滤波器得到高频分量。

离散小波变换进行2级分解的示例结构

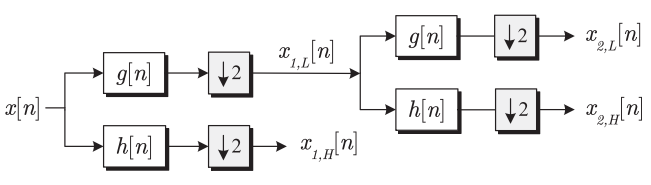
where g[n] is a low pass filter and h[n] is a high pass filter