支持向量机(Support Vector Machine,SVM)
支持向量机是我们用于分类的一种算法。
小故事理解SVM:
当一个分类问题,数据是线性可分的,也就是用一根棍就可以将两种小球分开的时候,我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可,寻找这个最大间隔的过程,就叫做最优化。但是,现实往往是很残酷的,一般的数据是线性不可分的,也就是找不到一个棍将两种小球很好的分类。这个时候,我们就需要像大侠一样,将小球拍起,用一张纸代替小棍将小球进行分类。想要让数据飞起,我们需要的东西就是核函数(kernel),用于切分小球的纸,就是超平面。
问题是从线性可分延伸到线性不可分的
线性SVM
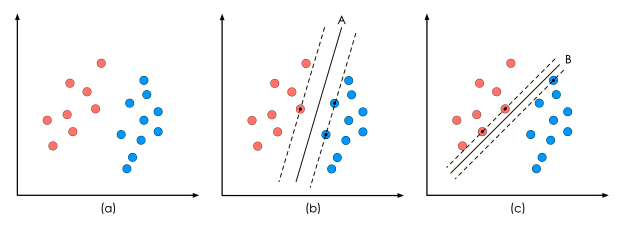
上图中的(a)是已有的数据,红色和蓝色分别代表两个不同的类别。数据显然是线性可分的,但是将两类数据点分开的直线显然不止一条。上图的(b)和(c)分别给出了B、C两种不同的分类方案,其中黑色实线为分界线,术语称为“决策面”。每个决策面对应了一个线性分类器。虽然从分类结果上看,分类器A和分类器B的效果是相同的。但是他们的性能是有差距的,看下图:
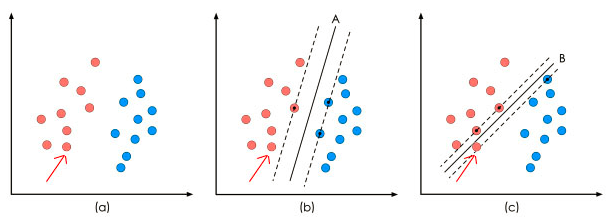
在”决策面”不变的情况下,我又添加了一个红点。可以看到,分类器B依然能很好的分类结果,而分类器C则出现了分类错误。显然分类器B的”决策面”放置的位置优于分类器C的”决策面”放置的位置,SVM算法也是这么认为的,它的依据就是分类器B的分类间隔比分类器C的分类间隔大。这里涉及到第一个SVM独有的概念”分类间隔”。在保证决策面方向不变且不会出现错分样本的情况下移动决策面,会在原来的决策面两侧找到两个极限位置(越过该位置就会产生错分现象),如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。显然每一个可能把数据集正确分开的方向都有一个最优决策面(有些方向无论如何移动决策面的位置也不可能将两类样本完全分开),而不同方向的最优决策面的分类间隔通常是不同的,那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点,就是SVM中的支持样本点,称为”支持向量”。
数学建模
决策面方程
分类间隔方程
约束条件
最优化问题的两个基本因素:
1.目标函数 你希望什么东西的什么指标达到最好
2.优化对象 你期望通过改变哪些因素来使你的目标函数达到最优
Example:
在线性SVM算法中,目标函数就是分类间隔,优化对象就是决策面
最优化问题的分类:
1.无约束优化问题 min f(x)
求解方法:费马大定理(求f(x)的导数,令其为0,求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解)
2.有等式约束的优化问题
min f(x)
s.t. hi(x)=0,i=1,2,…,n
求解方法:拉格朗日乘子法(把等式约束hi(x)用一个系数与f(x)写成一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为0,求得候选值集合,然后验证求得最优值)
3.有不等式约束的优化问题
min f(x)
s.t. gi(x)<=0,i=1,2,…,n
hj(x)=0,j=1,2,…,m
求解方法:拉格朗日+KKT条件 把所有的等式、不等式约束与f(x)写成一个式子,也叫拉格朗日函数,系数也称为拉格朗日乘子,通过一些条件可以求出最优值的必要条件,这个条件称为KKT条件。
KKT条件的全称是Karush-Kuhn-Tucker条件,KKT条件是说最优值条件必须满足以下条件:
条件一:经过拉格朗日函数处理之后的新目标函数L(w,b,α)对x求导为零:
条件二:h(x) = 0;
条件三:α*g(x) = 0;
使用拉格朗日方程的目的:
将约束条件放到目标函数中,将有约束优化问题转换为无约束优化问题(我们知道我们要求解的是最小化问题,所以一个直观的想法是如果我能够构造一个函数,使得该函数在可行解区域内与原目标函数完全一致,而在可行解区域外的数值非常大,甚至是无穷大,那么这个没有约束条件的新目标函数的优化问题就与原来有约束条件的原始目标函数的优化问题是等价的问题。)
使用拉格朗日获得的函数使用求导方法求解依然困难,进而需要对问题进行一次转换,即使用一个数学技巧:拉格朗日对偶(将最小值和最大值的计算位置交换)
拉个朗日优化问题的两个步骤:
1.将有约束的原始目标函数转换为无约束的新构造的拉格朗日目标函数
2.使用拉格朗日对偶性,将不易求解的优化问题转化为容易求解的优化问题
求解对偶问题的三个步骤:
1.首先要让L(w,b,α)关于w和b最小化
2.求对α的极大
3.利用SMO算法求解对偶问题中的拉格朗日乘子
SMO算法
1996年,John Platt发布了一个称为SMO的强大算法,用于训练SVM。SMO表示序列最小化(Sequential Minimal Optimizaion)。Platt的SMO算法是将大优化问题分解为多个小优化问题来求解的。这些小优化问题往往很容易求解,并且对它们进行顺序求解的结果与将它们作为整体来求解的结果完全一致的。在结果完全相同的同时,SMO算法的求解时间短很多。
SMO算法的目标:
求出一系列alpha和b,一旦求出了这些alpha,就很容易计算出权重向量w并得到分隔超平面。
SMO算法的工作原理是:
每次循环中选择两个alpha进行优化处理。一旦找到了一对合适的alpha,那么就增大其中一个同时减小另一个。这里所谓的”合适”就是指两个alpha必须符合以下两个条件,条件之一就是两个alpha必须要在间隔边界之外,而且第二个条件则是这两个alpha还没有进行过区间化处理或者不在边界上。
注意:
实际上,对于目标函数,是存在一个假设(数据100%线性可分)的,但现实中的数据都不那么干净,这时我们就可以通过引入松弛变量ξ(slack variable)和惩罚参数C来允许有些数据点可以处于超平面的错误的一侧—>约束条件的改变—>目标函数的改变
SMO算法优化
启发式选择第二个alpha值
非线性SVM
核技巧
对于非线性情况:SVM的处理方式是选择一个核函数。简而言之:在线性不可分的情况下,SVM通过某种事先选择的非线性映射(核函数)将输入变量映到一个高维特征空间,将其变成在高维空间线性可分,在这个高维空间中构造最优分类超平面。
建立非线性学习器分为两步:
1.首先使用一个非线性映射将数据变换到一个特征空间F;
2.然后在特征空间使用线性学习器分类。
核函数方法
在特征空间中直接计算内积 <ϕ(xi),ϕ(x)>的方法称为核函数方法
核是一个函数k,对所有x,z∈X,满足k(x,z)=<ϕ(xi),ϕ(x)>,这里ϕ(·)是从原始输入空间X到内积空间F的映射。
简而言之:如果不是用核技术,就会先计算线性映ϕ(x1)和ϕ(x2),然后计算这它们的内积,使用了核技术之后,先把ϕ(x1)和ϕ(x2)的一般表达式<ϕ(x1),ϕ(x2)>=k(<ϕ(x1),ϕ(x2) >)计算出来,这里的<·,·>表示内积,k(·,·)就是对应的核函数
将内积替换成核函数的方式被称为核技巧(kernel trick)。
总结
SVM的优缺点
优点:
1.可用于线性/非线性分类,也可以用于回归,泛化错误率低,也就是说具有良好的学习能力,且学到的结果具有很好的推广性。
2.可以解决小样本情况下的机器学习问题,可以解决高维问题,可以避免神经网络结构选择和局部极小点问题。
3.SVM是最好的现成的分类器,现成是指不加修改可直接使用。并且能够得到较低的错误率,SVM可以对训练集之外的数据点做很好的分类决策。
缺点:对参数调节和和函数的选择敏感。

